Puertas cuánticas

En el marco de la computación cuántica, llamamos puertas cuánticas a unos elementos que cuando reciben una señal de entrada nos dan otra de salida. Por lo tanto las puertas cuánticas tendrán unos elementos de entrada par recibir la información que nosotros les damos y otros de salida para devolvernos los datos que correspondan, siendo el número de elementos de la entrada igual al de la salida.

Entre ambos, entrada-salida, dibujamos una caja negra que representa a unos circuitos electrónicos que a nosotros no nos interesan, porque para nosotros las puertas no son circuitos reales sino sus respectivas funciones lógicas. Partiendo al inicio de todas las entradas en estado |0>, y manejando una variedad reducida de puertas lógicas debidamente conectadas, podemos llevar a cabo un número incalculable de posibles aplicaciones. Veamos algunas de estas puertas cuánticas.

Puerta X.- Transforma el estado |0> en estado |1> y viceversa. En la superposición aplica esto mismo a cada uno de los estados posibles. Se escribe así:

Como no se han puesto flechas, leeremos siempre de izquierda (entrada) a derecha (salida). Esta puerta es matemáticamente equivalente a aplicar el operador

Y lo mismo se podrían comprobar las otros dos. Recordemos que, debido al carácter vectorial de los estados cuánticos, esta notación matricial de un estado cuántico es equivalente a la notación tradicional. Por ejemplo,

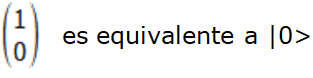
Puerta Z.- Esta puerta es igual de sencilla que la anterior y transforma |+> en |-> y |-> en |+>. Esta puerta, como la anterior y todas las que siguen, tiene también su operador matricial.

Puerta H o puerta de Hadamard.- Transforma de la siguiente manera:

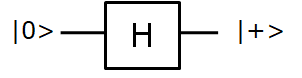
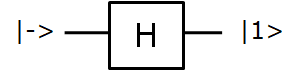
Podemos recordar que, |+>=|0>+|1> y |->=|0>-|1>. Como se ve la puerta es reversible y su operador matemático es el siguiente:

El factor uno partido por raiz de dos que se antepone a la matriz indica que al ser |+> = |0>+|1> los dos estados son equiprobables y la suma de ambas probabilidades es igual a uno.

Puerta CNOT.- Las dos puertas, X y H, son puertas de un solo cúbit, con una sola entrada y una sola salida. Veamos ahora una de dos cúbits llamada puerta CENOT, con dos entradas y dos salidas. A los estados cuánticos les podemos poner un subíndice que haga referencia al cúbit 1 o al cúbit 2. Las posibilidades de entrada son las siguientes:

|0>₁|0>₂ ; |0>₁|1>₂ ; |1>₁|0>_{2 ;} |1>₁|1>₂

A estas entradas les corresponden las salidas de la figura 1.

En estas figuras al cubit de arriba, marcado con un punto, se le llama cubit de control y al de abajo, marcado con un círculo, cúbit objetivo. Lo que hace esta puerta es muy simple: Si el cúbit de control es |0>, el cúbit objetivo se queda como estaba; si el cúbit de control es |1>, se cambia el cúbit objetivo.

Puerta CCNOT.- Se trata de una ampliación para tres cúbits de la puerta CNOT, con dos cúbit de control y un cúbit objetivo Su circuito lógico es el de la figura 1.1

A este circuito lógico le corresponde la siguiente tabla de entradas-salidas.

A	B	C	A’	B’	C’
0	0	0	0	0	0
0	0	1	0	0	1
0	1	0	0	1	0
0	1	1	0	0	0
1	0	0	1	0	0
1	1	0	1	1	1
1	0	1	1	0	1
1	1	1	1	1	0

Medida.-Para indicar que hacemos una lectura utilizaremos el dibujo de la figura 2. Lo que indica la figura es que aunque el sistema esté evolucionando conforme a la ecuación de onda de Schrödinger, siendo Ψ la función de onda, la medida del estado de un cúbit siempre será un cero o un uno. No hay otra posibilidad.

Ejercicio.- Con todo esto ya podemos hacer la lectura de un pequeño circuito como el que nos propone el profesor Alberto Casas en su libro La Revolución Cuántica, que se recoge en la figura 3.

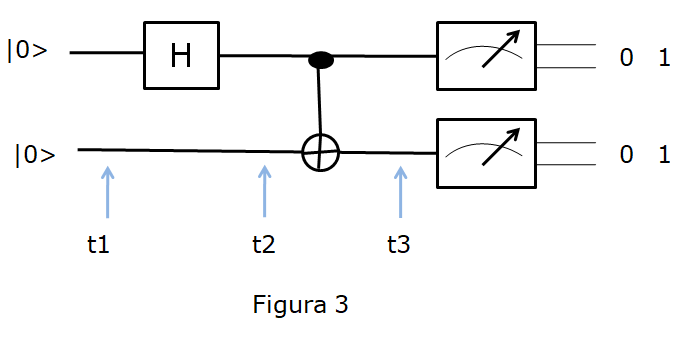
Como se ve se trata de un circuito de dos cúbits, que al comienzo del proceso, instante t1, están los dos en el estado |0>. Siempre se inicializan los procesos poniendo todos los cubits en este estado.

En el instante t2 el cúbit uno, tras superar la puerta H habrá pasado del estado |0> al estado |+>=|0>+|1>. El cubit dos seguirá en su estado inicial |0>. Pero aquí no se puede hablar de los estados de cada cubit por separado, como se hace en la computación clásica, ya que, por el principio de superposición, hay que hablar del estado global del sistema, que en este caso corresponde a:

(|0>₁ + |1>₁)|0>₂ = |0>₁|0>₂ + |1>₁|0>₂

Para pasar de t2 a t3 nos encontramos con una puerta CNOT, en la cual, como vemos en la figura 1, el grupo |0>₁|0>₂ que son las entradas de arriba se queda igual y el |1>₁|0>₂ se transforma en |1>₁|1>₂, quedando por lo tanto la situación global como:

|0>₁|0>₂ + |1>₁|1>₂

Esta es la situación del estado conjunto o estado global en el instante t3. Si ahora procedemos a la medida, el sistema colapsa en una de estas dos posibilidades y la medida tendrá que ser de dos ceros o dos unos, como indica la figura 3, sin que exista la posibilidad de medir arriba un cero y abajo un uno o viceversa.

Como los coeficientes que afectan a los dos términos son iguales a uno ambos medidas son equiprobables. Si en vez de esta expresión hubiéramos obtenido,

a|0>₁|0>₂ + b|1>₁|1>₂

las probabilidades de que el resultado de la medida fueran dos ceros o dos unos serían proporcionales a a²y b² respectivamente.

Con este ejemplo sencillo hemos viso la diferencia fundamental entre un circuito lógico clásico y otro cuántico. En los primeros podemos seguir paso a paso la evolución de los unos y los ceros de forma individualizada. En los segundos, debido a la superposición, hay que hacerlo siempre de forma global.

Y para terminar veamos como se puede hacer una suma, para lo cual recordemos que en un sistema binario la suma de la primera «decena» es como sigue:

0+0=0 ; 0+1=1 ; 1+0=1 ; 1+1=10, O bien, utilizando siempre dos dígitos:

0+0=00 ; 0+1=01; 1+0=01; 1+1=10

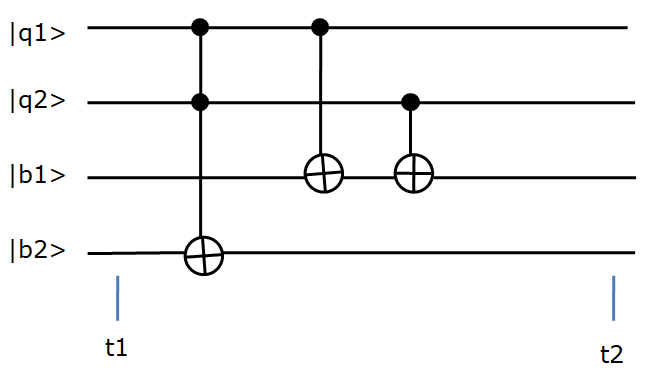
Figura 4

Trabajando con el circuito de la figura 4 y siguiendo la reglas dadas para las puertas tenemos lo siguiente:

Para una entrada en t1 de 0,0,0,0, los valores en t2 son: 0,0,0,0

Para una entrada en t1 de 0,1,0,0, los valores en t2 son: 1,1,1,0

Para una entrada en t1 de 1,0,0,0, los valores en t2 son: 0,1,1,0

Para una entrad a en t1 de 1,1,0,0, los valores en t2 son: 1,1,0,1

Leyendo las salidas en t2 de b2 b1 por este orden, tenemos que lo resultados son 00, 01, 01 y 10, que son las suma de las respectivas entradas q1 y q2.

La importancia de resolver el problema de la suma es enorme, pues, como nos enseñaron en el colegio, todas las funciones se pueden desarrollar en serie de Taylor, y, por lo tanto, conocer el circuito de la suma es el primer paso para calcular todo lo demás. El problema que ahora se presenta es, como ya se ha dicho, cómo leer en t2 solo los valores de b1 y b2 si las cuatro salidas están en superposición. Aunque ya dijimos algo sobre la medida de las salidas cuando vimos cómo construir un cúbit con microcircuitos superconductores, volveremos sobre este tema otro día.