Postulado Nº1 de la mecánica cuántica

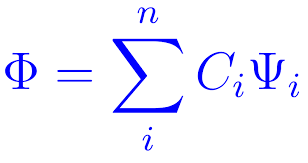
La Mecánica cuántica se asienta en varios postulados que generalmente forman un grupo de seis, aunque algunos autores los limitan a tres o cuatro. Veamos el que todos señalan siempre como el Postulado Nº 1 de la Mecánica cuántica.

El primer postulado establece que el estado cuántico de un sistema, por ejemplo, de una partícula que lanzamos contra una barrera de potencial, queda definido por un vector en el espacio de Hilbert, que recibe el nombre de vector de estado, del cual puede extraerse toda la información correspondiente a ese sistema.

¿Y qué es un espacio de Hilbert? Un espacio de Hilbert es una generalización abstracta de lo que conocemos como espacio vectorial, de n o infinitas dimensiones, cuyos componentes se diferencian de los componentes de los espacios vectoriales normales en que pueden ser números complejos, lo que da lugar a que los productos escalares o productos internos puedan ser reales o complejos. También, al igual que un vector se puede multiplicar por un número real dando lugar a otro vector, un vector de estado en el espacio de Hilbert  se puede multiplicar por un número complejo dando lugar a otro vector de estado en el espacio de Hilbert. 

Veamos cómo se escriben algunas de estas definiciones utilizando, cuando proceda, la nomenclatura cuántica:

 –Un vector A en un espacio vectorial normal de dos dimensiones, de componentes A₁, y A₂, referidas a una base e₁, y e₂, viene dado por:

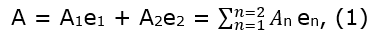
Siendo,

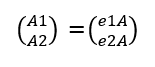
Donde e₁A es el producto escalar, de e₁ y A, y e₂A es el producto escalar de e₂ y A. En este espacio vectorial la base es ortonormal, porque los dos vectores e₁, y e₂ son unitarios y perpendiculares entre sí.

–Un vector de estado en un espacio vectorial de Hilbert de n dimensiones, de componentes complejos c_n referidos a una base de n elementos |u_n>, viene dado por:

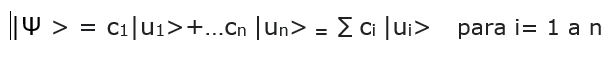
siendo,

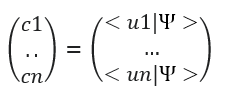
Donde <u₁|Ψ> es el producto escalar de u₁ y Ψ y <u₂|Ψ> es el producto escalar de u₂ y Ψ. El paralelismo entre los vectores y el carácter vectorial de los estados cuánticos en el espcio de Hilber es evidente.

Además de operar con vectores discretos como los mencionados, el espacio de Hilbert puede operar también con funciones de infinitas dimensiones que hacen las veces de vectores.

Veamos con un ejemplo cómo un estado cuántico puede representarse por un vector en el espacio de Hilbert:

Supongamos que tenemos una partícula de masa m en un pozo de potencial de anchura «a» como el de la figura1, del cual no puede salir porque las barreras que lo delimitan tienen un potencial de valor infinito que la partícula no puede superar. Para saber que ocurre con la partícula aplicamos la ecuación de onda de Schrödinger, que es una ecuación diferencial que nos da las siguientes soluciones para la propia función de onda y para la energía de la partícula:

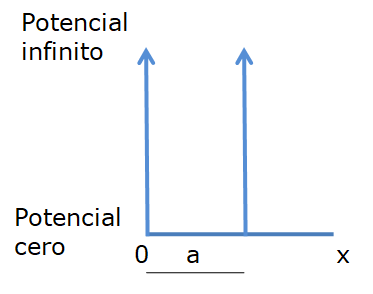
Figura 1

La figura 2 indica los valores de E_n y Ψ_n para n igual a 1, 2 y 3. Obsérvese que como n está al cuadrado en la fórmula, E₂=4E₁ y E₃=9E_1.

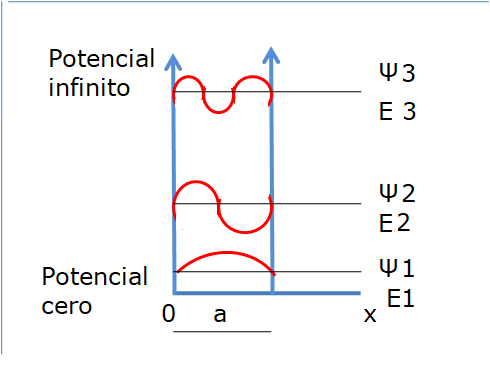
Figura 2

Dadas estas soluciones para la ecuación diferencial, se puede escribir como solución general de la ecuación de onda la siguiente:

Obsérvese que esto es parecido a los desarrollos en serie de Fourier pero al revés: aquí nos dan los componentes y sumándolos tenemos la función.

Esta estructura de Φ(x) tiene carácter vectorial, pues en ella:

Los valores de a_n equivaldrían a las componentes del vector A₁, A₂ de la fórmula  (1) y

Los valores Ψn(x) equivaldrían a las bases e1, e2 etc de la misma fórmula, que en este caso son funciones.

Lo que en vectores decíamos que era el producto interno e₁A=Ae₁, que es la componente de A sobre la base e₁, que es A₁, con notación cuántica sería:

Vemos pues que el sistema queda definido por un vector de estado, Φ(x), de n o infinitas dimensiones, en un espacio de Hilbert, cuya base está formada por los distintos valores de Ψ_n, con respecto a la cual las componentes de Φ, a_n, serán los productos internos de Φ por cada uno de los elementos de esta base, que es lo que expresa la fórmula (2)    

Si los valores de a_n fueran, por ejemplo, 2,5,7 etc. Y calculamos los valores de Ψ₁, Ψ₂, Ψ₃ etc integrando entre 0 y a, la función de estado sería:

|Φ> = 2 |Ψ₁> + 5 |Ψ₂> + 7|Ψ₃> etc., donde se aprecia mejor el carácter vectorial discreto del espacio de Hilbert para este caso concreto.

Si nos interesa definir un estado cuántico es para poder saber cuánto valen las variables que queremos conocer, variables que en mecánica cuántica reciben el nombre de observables. En el caso que hemos puesto, los observables son la energía y la posición de la partícula.