Principio de exclusión de Pauli

El principio de exclusión de Pauli fue enunciado por el físico austríaco Wolfgang Pauli en 1925, cuando el desarrollo de la física cuántica estaba en plena efervescencia. Su importancia es enorme y así lo entendieron enseguida todos sus colegas, aunque quizás no gozó de la popularidad de otros descubrimientos porque se le consideró como una aportación más entre las muchas que entonces se produjeron, y porque sus aplicaciones eran más técnicas que otras que interesaron más al gran público. Por el descubrimiento de este principio que lleva su nombre se le concedió el premio Nobel en 1945.

El estado cuántico de un electrón atrapado en un átomo está definido por cuatro números cuánticos denominados n, l, m_l y m_s. El número n indica su proximidad al núcleo y su energía; el número l indica la forma del espacio donde puede estar localizado, denominado orbital, y también posibles subniveles de energía; el m_l indica la orientación en el espacio del orbital; y el m_s indica el espín, que puede tomar los valores de más menos ½.

En su aplicación más divulgada el principio de exclusión de Pauli dice que en un mismo átomo, no puede haber dos electrones con los cuatro números cuánticos iguales. Si decimos que estos números definen el estado cuántico de cada electrón, esto quiere decir que no puede haber dos electrones cuyos estados cuánticos sean idénticos. Aquí se suele citar como referencia del mundo macroscópico el principio de impenetrabilidad, que dice que dos sólidos no pueden ocupar el mismo lugar al mismo tiempo. A continuación se recogen en seis columnas los números cuánticos correspondientes a los seis electrones del carbono. A cada electrón le corresponde una columna, y como se puede ver no hay dos electrones que tengan iguales sus cuatro números cuánticos.

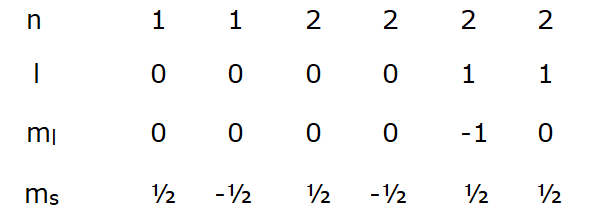
El principio de exclusión de Pauli tiene una formulación matemática interesante. Supongamos que tenemos un sistema con dos partículas cuya función de onda ψ( x₁,y₁,z₁,x₂,y₂,z₂ ) describe la probabilidad de que etas partículas se encuentren en los puntos x₁,y₁,z₁ y x₂,y₂,z₂ respectivamente, que vendrá dada por el valor de ψ². Para simplificar la escritura de esta función la llamaremos ψ(1,2). Esta función puede ser:

Simétrica, en cuyo caso, 

ψ(2,1) = ψ(1,2),

Antisimétrica, en cuyo caso,

ψ(2,1) = – ψ(1,2),

Mixta, en cuyo caso, ψ(2,1) no es igual

ni a ψ(1,2) ni a – ψ(1,2)

Con esta formulación matemática, el principio de exclusión de Pauli se  enuncia diciendo que todas las funciones que representen estados de dos electrones tienen que ser de la variedad antisimétrica.

Si las dos partículas, como sistemas independientes, tuvieran por funciones de onda respectivamente

u(1) y v(2) La función ψ(1,2), en principio, sería,

ψ (1,2) = u(1) * v(2),                            (1)

que satisface las leyes estadísticas de las probabilidades, que dicen que la probabilidad de la función conjunta, que viene dada por ψ², es el producto de las otras dos probabilidades, que serían u² y v². Pero esta fórmula (1), en general, no es antisimétrica y por lo tanto no cumple con el principio de exclusión de Pauli, por lo cual hay que transformarla, y la única forma de hacerlo es convertirla en esta otra:

 ψ (1,2) = u(1) * v(2) – u(2) * v(1)        (2)

que sí es antisimétrica como se comprueba fácilmente. Por lo tanto, aunque por el cálculo de probabilidades podríamos pensar que la función de onda correspondiente a dos electrones independientes podría ser del tipo de la fórmula (1), la restricción de Pauli exige una definición como la que establece la fórmula (2). Pero esta función se anula cuando las funciones u y v son iguales, lo que quiere decir que la probabilidad de todo estado compuesto formado con estados individuales iguales es cero, que es precisamente lo que dice el enunciado que hemos visto en primer lugar: la probabilidad de que dos electrones tengan los cuatro números cuánticos iguales es cero. Estamos pues ante la exclusión de que en determinadas condiciones puedan existir dos estados individuales idénticos.

La ecuación (1) corresponde al caso general, cuando las partículas no ejercen ninguna correlación entre sí: el estado de varios sistemas físicos no interactuantes es siempre un único producto de los estados de los sistemas individuales. Y también es cierto el enunciado inverso: si un estado no reviste forma de producto tiene que representar a individuos interactuantes, o lo que es lo mismo, implica una correlación entre los sistemas. Por lo tanto, como la fórmula (2) no es un simple producto implica la existencia de correlaciones entre las partículas, que no pueden ser otra cosa que la existencia de fuerzas entre ellas, aunque estas fuerzas no sean de origen dinámico. Como si cada partícula quisiera estar sola y huyera de la otra.

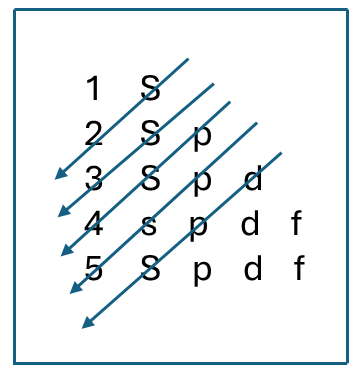
Figura de cabecera: Esquema del gráfico de Moeller o de las diagonales que se utiliza para determinar la configuración electrónica de los átomos por niveles de energía.