Emmy Noether fue una matemática alemana de ascendencia judía que nació en Baviera 1882. Los matemáticos la recuerdan por sus trabajos de álgebra y los físicos por un teorema sobre cantidades conservadas que lleva su nombre. Por su condición de mujer fue marginada en los ambientes académicos.
Sin embargo, Emmy Noether tuvo la suerte de asistir en Gotinga a las clases de tres de los grandes: Schwarzschild, Minkowski y Hilbert. Es imposible hablar de la teoría de la relatividad general sin mencionar estos tres nombres. Einstein dijo de ella que era la mejor matemática de su tiempo. También tuvo ocasión de asistir a algunas clases de su padre, Max Noether, reconocido matemático y profesor de universidad.
El teorma de Noether dice que cuando un sistema físico presenta una o varias simetrías, cada una de ellas lleva asociada una cantidad conservada y viceversa. ¿Qué son las simetrías de un sistema físico y qué son las cantidades conservadas?
Supongamos que vamos caminando por un sendero abierto en el interior de una plantación de maíz. A izquierda y derecha solo veré unas plantas de maíz cuya altura es mayor que la mía. Si camino cien o doscientos metros, veré exactamente lo mismo, hasta el punto de que si me hubieran vendado los ojos para el traslado, ni siquiera podría saber si he cambiado de sitio. Esto sería una simetría longitudinal. De forma análoga podríamos hablar de una simetría circular si me encuentro en medio de un desierto un día sin sol. Mire para donde mire a mi alrededor, girándome 360 grados, siempre veré lo mismo. Y si estoy leyendo en mi casa con las ventanas cerradas, siempre que levante la vista del libro tendré delante de mí los mismos muebles y enseres a lo largo de toda la tarde, con independencia de que sean las tres o las siete. Esto sería una simetría temporal. En estos tres ejemplos lo que se conserva es siempre lo mismo: el panorama que tengo delante de mí. En física lo que se conservaría en estos tres casos serían el momento lineal, el momento angular y la energía.
Cualquier experimento que queramos estudiar en física tenemos que situarlo dentro de un espacio donde podamos hacer medidas, y lo que define la capacidad de un espacio para medir es su métrica. La métrica de un espacio se define por una matriz cuyos elementos pueden variar de un punto a otro. Un espacio sin métrica es un espacio inútil para hablar en él de distancias, velocidades, fuerzas o energía. Para ver cómo varía la métrica en una dirección dada basta con derivarla con respecto a un vector unitario que marque esa dirección. Entonces puede ocurrir que haya direcciones con respecto a las cuales la métrica no varíe. Es decir, direcciones con respecto a las cuales la derivada de la métrica sea nula y en consecuencia la métrica se mantenga constante. Los vectores que marcan estas direcciones se llaman vectores de Killing y se suelen representar por el símbolo ξ. En un espacio de n dimensiones el número máximo de vectores de Killing es de n*(n+1)/2. En consecuencia, en un espacio-tiempo de cuatro dimensiones habrá un máximo de diez vectores de Killing, es decir diez direcciones a las que les corresponderán diez magnitudes conservadas.
Pero lo mismo que puedo calcular el vector de Killing en un punto, puedo calcularlo en el siguiente según la dirección que él mismo marca, después en otro y así sucesivamente hasta construir un campo de vectores de Killing, que me indicará en cada punto la dirección en la que podemos ir avanzando sin que cambie la métrica. Este campo tiene unas propiedades interesantes y entre ellas se encuentra la de que se mantienen las distancias.
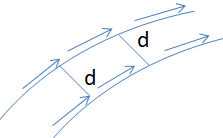
Que se mantengan las distancias quiere decir que si parametrizamos la familia de curvas conforme a un parámetro λ, y la distancia entre dos puntos de dos curvas diferentes cuando λ sea igual a λ1 es d, cuando λ tome otro valor, por ejemplo λ2 , la distancia entre esos dos puntos seguirá siendo d, como indica la figura. Esto significa que nos hemos desplazado por las curvas del campo de vectores de Killing a velocidad constante. Por lo tanto, ya tenemos la forma de ver qué cantidades se conservan: igualando a cero la derivada de la métrica calculamos los vectores de Killing, hacemos el producto escalar de cada uno de ellos por la velocidad, u, derivamos, igualamos a cero esta derivada y a ver que sale.
Aunque esto es conceptualmente sencillo, los cálculos, como todos los cálculos relacionados con la teoría de la relatividad general, son laboriosos. El resumen de los resultados que se obtienen en el espacio-tiempo de Minkowski de cuatro dimensiones, e0, e1, e2 y e3 es el siguiente:
-El eje temporal e0 marca una simetría temporal en la que se conserva la energía.
-Los tres ejes espaciales e1, e2, y e3 marcan simetrías longitudinales en las que se conserva el momento lineal.
-Tres vectores de Killing nos indicarán simetrías rotacionales en torno a los tres ejes espaciales e1, e2 y e3 con conservación de los momentos angulares.
-Los tres vectores de Killing restantes, relacionan el eje temporal con cada uno de los ejes espaciales y hacen referencia a la conservación del momento angular relativista.
Como se ve, el alcance de este teorema es importante.
En 1933, el gobierno de Hitler le comunicó a Emmy Noether que no podía seguir enseñando en la Universidad de Gotinga, donde ejercía su magisterio docente, y como decenas de profesores se quedó sin empleo y empezó a buscar trabajo fuera de Alemania. Pronto empezó a dar clases en el Instituto de Estudios Avanzados de Princeton, donde tuvo una vida agradable y contaba con el apoyo de sus colegas. Desgraciadamente esta etapa duró poco, porque en 1935 le diagnosticaron una enfermedad que acabó con su vida ese mismo año. Sus cenizas se encuentran en el claustro de la biblioteca M. Cary Thomas en la ciudad de Bryn Mawr en Pensilvania.