Algoritmo de Grover

El algoritmo de Grover es uno de los más utilizados en computación cuántica para buscar un número determinado en un conjunto de números desordenados. Algo así como buscar una bola blanca dentro de un conjunto de bolas negras. Si el número total de bolas es N, sin aplicar el algoritmo de Glover podría tener que hacer hasta N intentos o iteraciones. Aplicando el algoritmo de Glover el número máximo de intentos posibles se reduce aproximadamente a la raiz cuadrada de N.

Esto siginifica que si N es igual a un millón, sin aplicar el algoritmo podríamos tener que hacer hasta 1.000.000 de iteraciones y si lo aplicamos esta cantidad se reduciría a 1.000. Teniendo en cuenta la cantidad de búsquedas que se hacen al día y el número fuertemente creciente de elementos entre los que hay que buscar, el interés de aplicar este algoritmo es evidente.

En computación cuántica el ejemplo que hemos puesto equivale a encontrar un determinado estado cuántico |W> en una superposición |s>, de N estados cuánticos totales, que son los que corresponden a un sistema de n cubits en el que coexisten N=2ⁿ estados cuánticos superpuestos. Como hemos llamado |s> a la superposición de todos los estados, que son N, llamemos |s’> a la superposición de todos los estados menos el estado que buscamos, |W>, que son N-1. Es decir: número total de estados posibles, |s>; el estado que buscamos, |W>; resto de estados, |s’>.

Se tiene que cumplir por lo tanto que:

|s>= α |W> + β |s’> , (1)

siendo alfa la densidad de probabilidad de que al hacer una medida encontremos el estado |W>, que será tanto más pequeña cuanto mayor sea N ya que |W> es un estado simple, y |s’> es la superposición de todos los demás.

Si representamos esto en coordenadas cartesianas tendremos la figura que se dibuja más abajo, en la que tenemos el vector |s> como suma de |W> y |s’> multiplicados por las componentes α y β. Es importante observar que el ángulo que forman |s> y |s`> es θ.

Lo primero que hace el algoritmo de Grover es transformar el vector |s> en el vector |p>, que es su imagen trazando la perpendicular a |s’>, y a continuación buscar la imagen de |p> a través de la perpendicular a |s>, vector que hemos llamado |a>. Entonces nos encontramos con que:

|a> = α’ |W> + β’ |s’>

Como vemos, el ángulo que ahora forman |a> y |s> es 2θ, lo que quiere decir que nos vamos acercando al eje vertical. Cuando después de muchas iteraciones el valor inicial de θ siga creciendo, llegará un momento en el que el correspondiente vector |a> se identificará con el vector |W>, entonces el valor de la correspondiente α’ será uno, y si la probabilidad de haber alcanzado |W> es igual a uno quiere decir que ese es el valor que estábamos buscando.

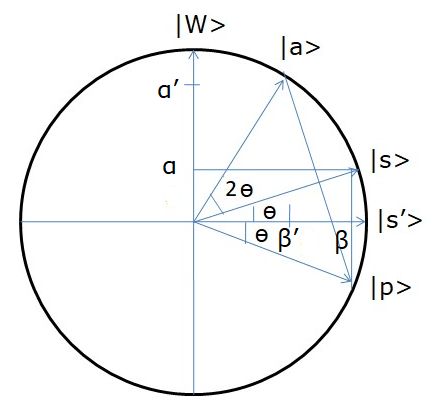
Veamos ahora cómo se obtiene que el número máximo de iteraciones es, aproximadamente, raiz cuzdrada de N. Como se ve en la figura en una iteración se gana un ángulo igual a 2θ. Esto significa que el número total de iteraciones para llegar hasta |W>, será el que nos permita recorrer un ángulo igual a (π/2 – θ), y por lo tanto, llamando r al número de iteraciones, se cumplirá que

r*2θ = π/2 – θ, de donde,

r=(π/2 – θ)/2 θ, (2)

Como hay N posibles estados cuánticos superpuestos, la probabilidad de que al medir salga el estado |W> será 1/N. Esto quiere decir que la densidad de probabilidad al cuadrado, fórmula (1), α² es igual a 1/N, y por lo tanto, como α²+ β²=1, que es la probabilidad total, β² = (N-1)/N. Además, como se ve en la figura, tang θ = α/β; a continuación se despeja θ y se sustituye arctang θ por θ, lo cual es lícito por tratarse de ángulos muy pequeños. Después se pone este valor de θ en la ecuación (2), y tras algunas aproximaciones se obtiene que el número de iteraciones está limitado por el valor de la raiz cuadrada de N. Partiendo de la ecuación 2 tendríamos:

r=(π/2 -θ)/2 θ =

= (π/2 – arctg α/β)/2 arctg α/β

r= (π/2 – α/β)/2α/β, y sustituyendo los valores de α y β y simplificando

llegaríamos a:
r = ((N-1)^1/2 -1) /4 ≈ ((N-1)^1/2π) /4 ≈

≈ (N-1)^1/2 ≈ N^1/2

Esta explicación geométrica tiene la ventaja de que es muy intuitiva. También tiene el encanto de fusionar entre sí la física cuántica y la geometría, lo cual no es de extrañar si recordamos que los estados cuánticos tienen carácter vectorial.

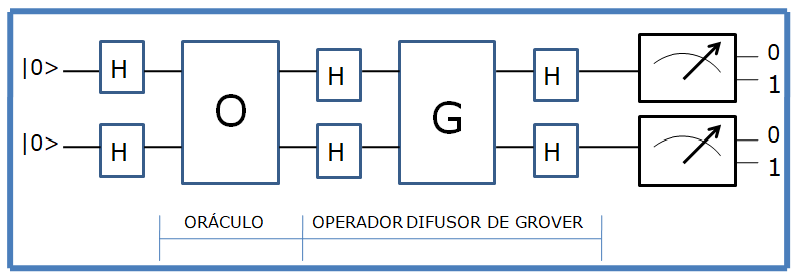
En la práctica esto se lleva a cabo con dos puertas cuánticas como se indica en la figura de cabecera. La primera puerta es una puerta de las llamadas Oráculo, que se llaman así porque su salida tiene la estructura de una respuesta a una pregunta. En este caso la puerta Oráculo trasforma la superposición de entrada |s> en la superposición de estados que en la figura hemos llamado |p>, que es una simetría respecto al eje horizontal. A continuación una puerta cuántica llamada puerta Grover transforma la superposición |p> en la superposición |a>, que como se ve es como una simetría sobre el vector |s> y está mucho más cerca del vector |W>.

Este algoritmo fue creado en 1996 por un informático nacido y formado en la India que trabajó luego en Estados Unidos, llamado Lov K. Grover. Su utilización con éxito en computación cuántica data de 2017. Su enorme valor, como ya hemos dicho, es la reducción cuadrática del límite superior de iteraciones a la hora de buscar un número en un conjunto desordenado de números, por ejemplo, encontrar un número de teléfono, sin saber a quien pertenece, en nuestra lista de contactos del teléfono móvil ordenada por orden alfabético de sus titulares.