Criptografía cuántica

El tema de la criptografía es de suma importancia. Para valorarlo no es necesario que pensemos en la famosa historia de la segunda guerra mundial cuando Alan Turing y sus muchachos trabajaban pare descifrar los mensajes cifrados por la máquina Enigma de los nazis alemanes. Ni tampoco en cómo la comunicación entre empresas o en el seno de la OTAN requiere de una reserva absoluta. Todas nuestras comunicaciones por guasap, nuestras comunicaciones con los bancos, nuestras transferencias o el uso de las tarjetas se realizan de forma cifrada.

Algunos historiadores piensan que «La Odisea» de Homero es un relato para transmitir mensajes encriptados sobre corrientes marinas, rutas, vientos y otros datos necesarios para la navegación de la época. Más conocido es el dato de que Julio César, usaba mensajes cifrados cambiando cada letra por otra situada dos puestos más adelante en el orden alfabético: en vez de una “a” utilizaba una “c”, o en vez de una “e” utilizaba una “g”. Ambos ejemplos son dos antecedentes curiosos para introducir el tema de la encriptación.

El método actual más utilizado data de 1979 y es el denominado RSA (Rivest, Shamir y Adleman), basado en la factorización de números enteros. Al emisor y al receptor los vamos a llamar Bob y Alice, que son los nombres que tradicionalmente se utilizan en física para personificar este tipo de relatos. Todos los mensajes se escriben con caracteres numéricos, ceros y unos, y el algoritmo comienza su andadura haciendo el producto de dos números primos, que se mantienen en secrteo, tan grandes como lo permitan nuestros medios de trabajo.

Cada uno de los usuaros del grupo con acceso al sistema tiene dos claves, una llamada pública, que la pueden conocer todos o algunos de los miembros del grupo, y otra privada que solo la conoce él mismo. Si Bob le quiere mandar un mensaje a Alice se lo envía escribiéndolo con la clave pública de Alice. Como este mensaje está escrito con la clave púbica de Alice, nadie puede descifrarlo salvo ella misma, que lo puede hacer con su clave privada.

Sin entrar en detalles matemáticos, una forma gráfica de contar cómo funciona el sistema RSA es la siguiente: Supongamos que la clave pública de Alice es una caja con un candado y que su clave privada es la llave de ese candado. Cuando Bob escribe un mensaje para Alicia lo que hace es pedirle su clave pública, es decir, meter el mensaje en la caja y cerrar el candado. El mensaje queda así oculto para todo el mundo excepto para Alice que tiene la llave del candado.

Este sistema es muy seguro, y tanto más cuanto mayores sean los números primos que utilicemos, cuyo techo queda impuesto por los ordenadores clásicos actuales. La computación cuántica nos permite trabajar con este sistema utilizando números primos cada vez más grandes. Otro sistema que se utiliza en la computación cuántica es el llamado BB84, creado por Charles Bennett y Gilles Brassard en 1984, basado en el comportamiento cuántico de los qubits.

El fundamento de este método es el siguiente: Si yo codifico un texto escribiéndolo a base de ceros y unos y le sumo una clave aleatoria de ceros y unos de la misma longitud, el resultado es un número aleatorio y por lo tanto imposible de descifrar. Lo que necesito entonces es poder crear una clave aleatoria y mandársela a mi interlocutor, para que después de que yo haga la suma y le envíe el resultado él pueda deshacerla y leer el texto original. Para enviar la clave sin que nadie pueda detectarla Bennett y Brassard fueron los primeros en utilizar conceptos de física cuántica.

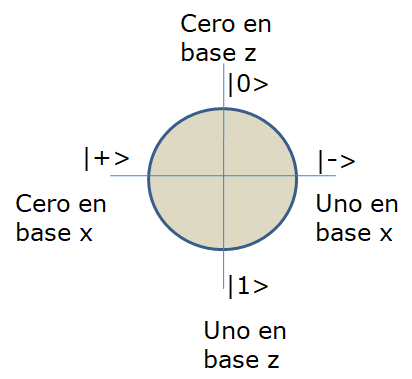
Supongamos que Alicia desea mandarle una clave a Bob. Lo primero que tiene que hacer es crear una clave aleatoria por cualquier procedimiento que ella conozca, por ejemplo lanzando una moneda al aire o utilizando un ordenador. A continuación transforma los unos y los ceros en estados cuánticos utilizando indistintamente la base z o la base x de la esfera de Bloch, en las cuales el 0 se transforma |0> o en |+> respectivamente, y el 1 se transforma en |1> o en |-> respectivamente, como se indica en la figura.

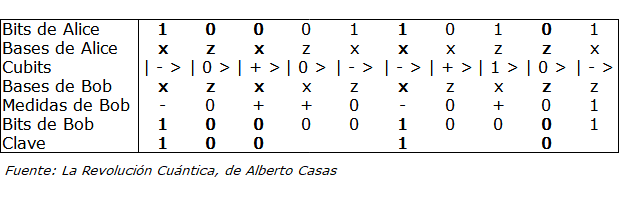
El resultado se lo manda a Bob, enviando los cúbits uno a uno. Bob los recibe y deshace lo que ha hecho Alicia, utilizando indistintamente y de forma aleatoria las dos bases z o x. A continuación Alicia le comunica a Bob por cualquier procedimiento abierto, ya que esto no entraña ningún riesgo, la secuencia de bases z o x que ella ha seguido. De los resultados que obtiene Bob, la clave deseada son aquellos números en los cuales coinciden las bases utilizadas por ambos, que se dará con una probabilidad del 50%. Este proceso se recoge en la tabla adjunta. Como se ve en la tabla las bases de Alice y Bob coinciden en las columnas 1(x,x), 2(z,z), 3(x,x), 6(x,x), y 9(z,z). Los números correspondientes a estas coincidencias (1,0,0,1,0) escritos en la última fila de la tabla, serán la clave compartida, con la cual Alicia puede enviar su mensaje a Bob sin que nadie pueda descifrarlo.

Este protocolo BB84 es sumamente seguro, y les permite a Bob y Alice crear una clave aleatoria compartida cada vez que necesiten enviarse un mensaje. Y si alguien interceptara su comunicación ambos detectarían que estaban siendo espiados. Su alto nivel de seguridad lo hace apto para comunicaciones cifradas entre gobiernos y toda clase de instituciones. Ya existen empresas que facilitan la creación de este tipo de claves cuánticas.