Invariancia

Los fenómenos de la naturaleza son de una determinada manera con independencia de que nosotros los observemos desde un sitio o desde otro. Esto, naturalmente, se puede aplicar a las leyes de la física, de las que decimos que son independientes del sistema de referencia desde el que nosotros hagamos nuestras medidas.

Esta afirmación se entiende bien conceptualmente y nadie la discute. Sin embargo, como la física se estudia mediante formulaciones matemáticas, hay que tener mucho cuidado para hacer siempre transformaciones coherentes que no nos lleven al engaño. Si estoy siguiendo el movimiento de un avión, no puedo medir unos tiempos desde dentro del avión, otros desde un caza que pasara por allí, y otros desde tierra y tratarlos todos revueltos como si fueran medidas hechas desde un sistema de referencia único. Las tres medidas pueden ser válidas pero tengo que tener en cuenta la posiciones desde las que se han tomado.

Un ejemplo de que las leyes de la física tienen que ser invariantes ante un cambio de ejes es la medida del módulo de un vector. Si tenemos un vector pintado en el suelo y lo mido acercándome a él con una cinta métrica, su módulo, es decir, lo que mide el vector de una punta a otra, tiene que ser el mismo que si lo medimos desde una azotea o una torre utilizando otros instrumentos.

Veamos un ejemplo. Supongamos que queremos estudiar un fenómeno físico representado por el vector A de la figura 1. Por las matemáticas de bachillerato sabemos que este vector, referido a la base e₁ y e₂, es, por ejemplo, el vector A = 4e₁+2e₂ siendo 4 y 2 sus componentes. Si para analizar mejor este fenómeno físico, este vector, nosotros necesitáramos que sus componentes fueran mayores que 4 y 2, ¿qué podríamos hacer? Pues mirarlo desde otro punto de vista, desde un punto de vista que nos permita apreciar lo que queremos, y para ello haríamos un cambio de base, de manera que, referido a esta nueva base, las componentes del vector fueran las que nosotros necesitamos.

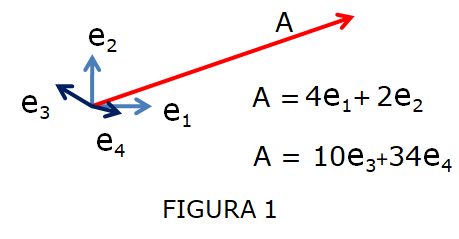
Esto lo podemos hacer con facilidad. Lo primero que tenemos que hacer es ver cómo transformamos las componentes del vector para obtener los valores que necesitamos. Lo hacemos buscando la matriz correspondiente y obtenemos que estas componentes son, por ejemplo, 10 y 34. A continuación a partir de esa matriz tansformamos la base y de esta manera tendríamos una nueva base e₃ y e₄ dada por:

e₃ = – ⅞ e₁ + ⅝ e₂

e₄ = ⅜ e₁ – ⅛ e₂

Con esto ya tenemos lo que buscamos, pues aunque referidos a bases distintas los dos vectores son el mismo vector:

4e₁+ 2e₂ = 10e₃+34e₄

Basta sustituir e₃ y e₄ por sus valores en función de e₁ y e₂ para comprobar que se trata del mismo vector. Hemos observado el fenómeno y hemos hecho nuestras medidas desde dos observatorios diferentes, obteniendo el mismo resultado. El fenómeno físico no ha cambiado y el módulo del nuevo vector será el mismo que el del vector anterior. Estamos viendo el mismo fenómeno físico desde distintos ejes de referencia.

Entre las transformaciones que se utilizan en física para hacer este tipo de cosas, una de las que más se utilizan es la llamada Tansformación de Lorentz, que es una transformación de coordenadas que tiene en cuenta que la velocidad de la luz es constante. Al considerar que la velocidad de la luz es constante nos encontramos con que el tiempo y el espacio no son independientes. Sin embargo, normalmente no se trabaja con cuatro dimensiones, sino que generalmente es suficiente trabajar con la coordenada temporal que llamamos x₀ y solo una de las tres coordenadas espaciales, que llamamos x₁. Si hacemos una transformación de Lorentz para pasar del sistema de coordenadas x₀, x₁ a un nuevo sistema x₀’ y x₁’ y empezamos a jugar un poco con las ecuaciones que van saliendo al paso, nos encontramos con lo siguiente:

– (∆x₀ )² + (∆x₁)² = – (∆ x₀’)² + (∆x₁’)²

Esto quiere decir que el resultado de aplicar esta ecuación, sea el que fuere, siempre da lo mismo ante una transformación de Lorentz, porque da lo mismo en el sistema x_0,x₁ que en el sistema x₀’,x₁’ . Por este motivo se dice que lo que quiera que sea esto es un invariante ante transformaciones de Lorentz.

En este caso, además, se trata de un invariante muy importante porque como se indica en la figura 2, en coordenadas cartesianas quitando el signo menos sería la medida de un incremento de arco, ∆S, mientras que en el espacio-tiempo esta expresión nos da el incremento de arco pero con un signo menos en la coordenada temporal, lo que supone un cambio de enorme importancia en este tipo de coordenadas. Este signo menos, que nos deja un poco desconcertados, es de enorme importancia en la teoría de la relatividad general y en la teoría cuántica de campos.

Con estos ejemplos hemos puesto de manifiesto la importancia de lo que los físicos llaman un invariante: en el primer caso haciendo alusión a la invariancia de las leyes de la física con independencia del lugar desde donde las observemos, y en el segundo haciendo alusión a la invariancia del valor de cualquier expresión matemática ante un cambio de coordenadas, pues cuando esto sucede, es porque tenemos delante algo importante que merece ser investigado.

Figura de cabecera: Matriz de la Transformada de Lorentz