Computación Cuántica

Siempre que se habla de la cronología de los ordenadores cuánticos se cita, entre otros hitos, una conferencia que dió en 1981 el físico estadounidense Richard Feynman (1918-1988, Premio Nobel de Física 1965) en el Instituto Tecnológico de Massachusetts, donde dijo que la naturaleza es cuántica y por lo tanto si queremos acercarnos a ella y simularla en algún tipo de ordenador tendríamos que abandonar la idea de hacerlo en un ordenador convencional, e ir pensando en la posibilidad de disponer de ordenadores cuánticos.

Iniciarse en la computación cuántica y desarrollarla después, aunque sea de forma muy resumida y a nivel de principiantes, no es tarea fácil. Y por supuesto es imposible hacerlo en un solo artículo. Por eso empezaremos hoy con este tema y volveremos sobre él de vez en cuando. En este asunto lo único fácil es la definición: Se entiende por computación cuántica la que se lleva a cabo según las leyes de la mecánica cuántica.

Ya hablamos hace unos meses del cúbit y ese artículo puede ser nuestro punto de partida. Un cúbit se puede construir con un microcircuito superconductor en el cual la corriente puede circular en un sentido, en el contrario o en una superposición de ambos; con iones que pueden girar en un sentido, en el contrario o en una superposición de ambos; y también con fotones, que pueden polarizarse de dos formas distintas y en una superposición de ambas. En todos estos casos uno de los dos estados posibles se representa por un cero o una flecha hacia arriba y el otro por un uno o una flecha hacia abajo, y para indicar que se trata de estados cuánticos estos símbolos se representan siempre encerrados entre una barra vertical y un signo >.

A uno de los dos estados cuánticos posibles siempre lo representaremos así, |0>, o con una flecha hacia arriba en lugar del 0.

Al otro estado cuántico posible lo representaremos así: |1>, o con una flecha hacia abajo en lugar del 1.

La superposición de ambos la representaremos así: a|0>+b|1>, donde a y b pueden tomar cualquier valor. El cuadrado de a es la probabilidad de que al medir el sistema se manifieste en el estado |0>, y el cuadrado de b la probabilidad de que lo haga en el estado |1>. La suma de los cuadrados de a y b, que son las dos únicas opciones posibles, tiene que ser 1.

Dado el carácter vectorial de los estados cuánticos, si representamos los valores de a y b como un vector columna,

El estado |0> corresponderá a los valoes de a=1 y b=0, y el estado |1> a los valores de a=0 y b=1, y se podrán representar como:

Otra notación importante es la que se utiliza cuando a y b valen uno. Estos dos estados se representan por |+> y |->, y valen por tanto:

|+> = |0>+|1>

|->=|0>-|1>

Aunque esto suele escribirse de esta manera, en rigor, para que la suma de los cuadrados de a y b sea uno, estos coeficientes que aquí hemos puesto iguales a uno tendrían que ser uno partido por raiz de dos.

Todas estas notaciones son fáciles y hay que habituarse un poco a ellas.

Cada cúbit puede trabajar no solo con sus dos estados |0> y |1> en superposición, sino que además puede trabajar en superposición con los estados de los demás cúbit del ordenador. El lugar geométrico de los posibles estados a|0>+b|1> es una esfera llamada Esfera de Bloch, como la de la figura, que tiene como puntos singulares los marcados con las flechas hacia arriba, hacia abajo, hacia la derecha y hacia la izquierda, que correspoden a otros tantos sentidos de giro de los iones.

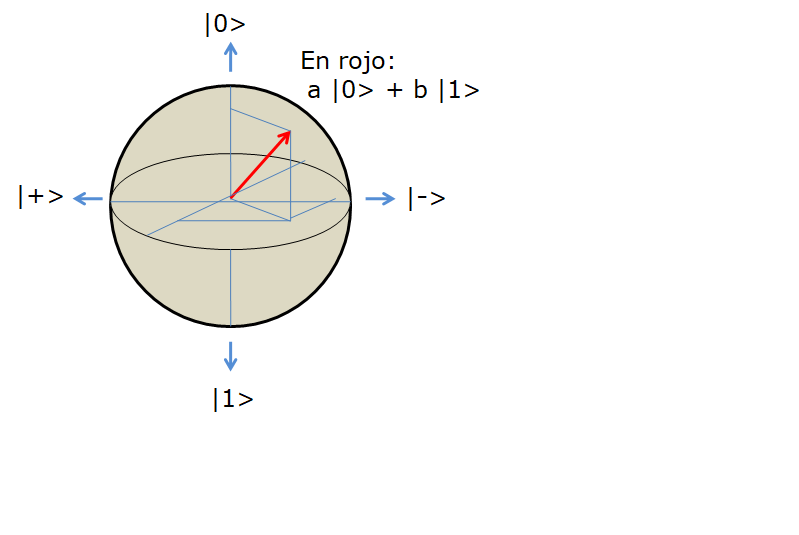
Esta esfera es por lo tanto una representación geométrica del espacio de estados de un sistema cuántico. Si hiciéramos una medida en el momento marcado por el vector en rojo, si estuviéramos midiendo la componente del eje vertical sería más probable que el sistema colapsara en el estado |0> que en el estado |1>, y si lo hiciéramos en el eje horizontal sería más probable que colapsara en el estado |-> que en el estado |+>. En el plano ecuatorial de la figura los posibles colapsos en |0> o |1> son equiprobables

En el artículo del cúbit vimos que para estudiar o diseñar una configuración de un ordenador clásico no se utilizaban circuitos reales con transistores, resistencias y semiconductores, sino que se utilizaban lo que podríamos llamar circuitos lógicos, construidos con elementos que reciben el nombre de puertas, y que cualquier configuración por complicada que sea se puede desarrollar con un entramado complejo y laborioso utilizando una variedad pequeña de estas puertas. En la computación cuántica las puertas se llaman naturalmente puertas cuánticas. También vimos en el artículo del cúbit que, gracias a la superposición, en un ordenador cuántico con n cúbits se pueden hacer simultáneamente 2ⁿ operaciones diferentes de forma simultánea, mientras que con un ordenador clásico habría que hacerlas una a una. Y aquí es donde conviene dejar hoy clara la importancia de este dato.

Una multiplicación de dos números de n cifras requiere hacer n² multiplicaciones simples. Cuando crece n, a este tipo de crecimiento se lo denomina crecimiento polinómico. En cambio, una factorización de un número de n cifras requiere de un número de operaciones simples que crece de forma exponencial, como la indicada de 2ⁿ. Si trabajamos con números grandes la diferencia es enorme. De aquí se deduce que hacer un cálculo de cualquier cosa que crezca exponencialmente con n cuando n sea un número de muchas cifras es prácticamente imposible con un ordenador clásico que las hace de una en una, y más fácil con un ordenador cuántico que las hace todas simultáneamente.

Pero aquí surge un problema. El principio de superposición nos dice que cuando un sistema cuántico va evolucionando lo va haciendo desarrollando simultáneamente todas las soluciones posibles, pero que cuando hacemos una medida ésta nos da solo la medida de una de una de esas soluciones, mientras que todas las demás desaparecen y el sistema queda en el estado que hemos medido. Técnicamente se dice que el sistema colapsa en solo uno de sus estados posibles. Por lo tanto, de nada nos sirve hacer 2ⁿ operaciones simultáneas si solo podemos obtener el resultado de una de ellas.

Esto se agrava un poco más si se tiene en cuenta que la superposición puede romperse por una interacción de los cubits con el mundo exterior, y que esta interacción no solo tiene lugar cuando hacemos una medida sino también cuando cambia alguna de las variables que definen el medio ambiente, dando lugar a alteraciones del propio sistema que pueden ser una fuente importante de errores.

Con todo lo anterior hemos abierto los temas que tendremos que ir desarrollando: cuáles son las aplicaciones más importantes que requiere el enorme potencial de cálculo de un ordenador cuántico; cómo se manejan las puertas cuánticas; cómo se solucionan los problemas mencionados debidos al colapso; o qué algoritmos matemáticos ayudan a manejar tanta información como aquí se utiliza. Y, por supuesto, cómo avanza esta carrera de la computación cuántica emprendida por grandes empresas y grandes países utilizando distintos tipos de cúbits. Todo esto hay que verlo despacio para ir asimilando lo que vayamos aprendiendo.

Fotografía: Computadora cuántica de Microsoft